Exercices Circuit logique et table de vérité et Algèbre de boole et table de Karnaugh ( avec Corrigés )
Objectifs : - Définir les opérations logiques fondamentales.
- Représenter physiquement un circuit logique.
- Utiliser la logique de boole.

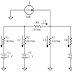
Exercice 2 : Quelle est la fonction logique réalisée par le circuit de la

Exercice 3 : Quelle est la fonction logique réalisée par le circuit de la figure suivante :

Exercice 4 : Utilisez l'algèbre de Boole pour simplifier les équations logiques suivantes :

Exercice 5 : Utilisez la table de Karnaugh pour simplifier l'équation logique suivante :
Exercice 6 : On dispose de 2 nombres binaires x et y à 3 bits chacun tels que x = [x2x1x0] et y = [y2y1y0]. On veut concevoir un circuit
Exercice 7 : On désire effectuer la somme OU logique du contenu de deux registres A et B de 4 bits chacun selon l'équation suivante :
B <= A + B
C'est-à-dire que le résultat du contenu de A OU du contenu de B sera
1. établir la table d'état contenant les colonnes Ai et Bi au temps t, Bi au temps t+1 et les entrées du bistable R-S.
2. l'expression logique du circuit.
3. le schéma logique du circuit.
Exercice 8 : On demande de simplifier une fonction logique s définie par sa forme canonique et sa table de vérité telle que :
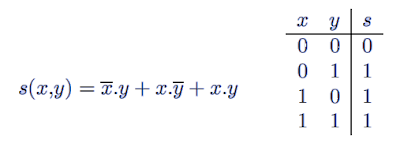
Exercice 9 : On demande de simplifier une fonction logique s définie par sa forme canonique et sa table de vérité telle que :

Corrections :
Le circuit logique et la

Solution de l'exercice 2 :
Le circuit réalisé la fonction ET telle que :

Solution de l'exercice 3 :
Le circuit réalisé la fonction OU telle que :

Solution de l'exercice 4 :
Solution de l'exercice 5 :
Solution de l'exercice 6 :
Les combinaisons possibles pour x et y sont de 23 = 8, c'est-à-dire :
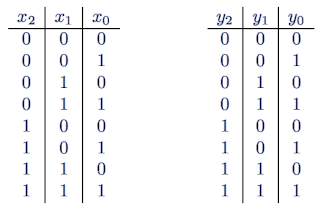
A chaque combinaison de x peut correspondre n'importe laquelle des huit combinaisons de y.
De plus, pour chaquebit xi il existe 2 combinaisons possibles de bits de y et inversement, de telle sorte que la solution par rapport à la comparaison bit par bit est :
De plus, pour chaque

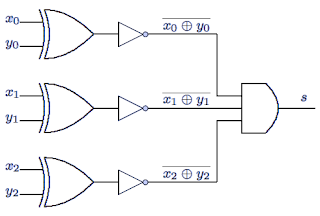
Comme chaque entrée est à 3 bits (bit 20, bit 21 et bit 22), et que chaque paire de bits est décrite par l'équation (1), alors le circuit cherché est le suivant :

L'équation (1) peut être simplifiée en ajoutant, sans rien changer à l'équation, deux zéros
 ainsi :
ainsi :
L'équation (2) donne un circuit qui ne nécessite que 7 éléments au lieu des 16 du circuit non simplifié tel que :
Solution de l'exercice 7 :
1. La table d'état est :

(0/1) veut dire que l'on peut indifféremment choisir soit 0 soit 1.
2. les

ce qui nous donne, pour chaque bit i,le schéma suivant :

3. le schéma logique complet du circuit est :

Solution de l'exercice 8 :
1. Simplification par voie algébrique :
le théorème d'idempotence permet d'écrire :

2. Simplification par la méthode de Karnaugh :
On reproduit la table de vérité dans une table, appelée table de Karnaugh, telle que :

On remarque que les 4 cases de la table de Karnaugh correspondent aux 4 lignes de la table de vérité. La simplification consiste à encercler tout ensemble de cases remplies de 1, adjacentes sur la même ligne ou la même colonne.
Dans notre exercice, on trouve deux ensembles (ligne y = 1 et colonne x = 1) de cases qui recouvrent complétement les parties affectées aux variables x et y.
Ainsi, on peut déduire que la solution est s = x + y.
Ainsi, on peut déduire que la solution est s = x + y.
Solution de l'exercice 9 :
La table de Karnaugh est :